一、考题回顾

教师资格证报名入口

1.题目：圆的面积

2.内容：

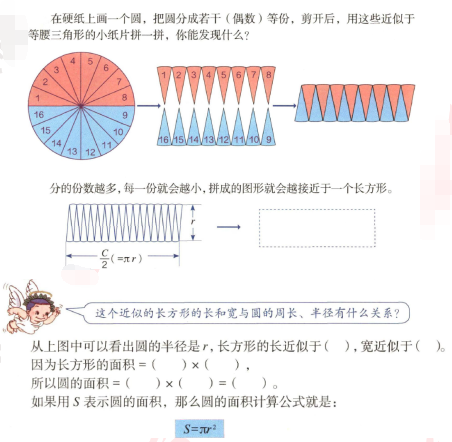
3.基本要求：

(1)引导学生极限、近似的转化思想;

(2)试讲过程有板书;

(3)十分钟内讲完。

答辩题目：1.简单说一说引导学生学习圆的面积?

2.对于圆的面积公式的推导过程体现了数学中的哪种思想方法?

二、考题解析

【教学过程】

(一)创设情景，导入新课

一只小狗被它的主人用一根长1米的绳子栓在草地上，问小狗能够活动的范围有多大?

问题：1.小狗能够活动的最大面积是一个什么图形?

2.如何求圆的面积呢?

(二)师生互动，探索新知

(1)引导：平行四边形面积可以转化成长方形面积，那么是否可以将圆转化成已学的图形呢?

(2)实验操作：教师将课前准备好的圆分给各小组(前后四人为一组)。请同学们试试看，是否可以将圆转化成为长方形。

(3)动画展示：

把圆分成4份、8份，然后拼图。

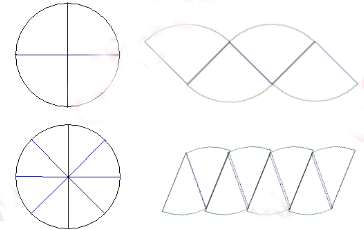
让学生闭起眼睛想一想是不是分得的份数越多拼成的图形越接近于长方形。

把圆16等分拼成近似的平行四边形。

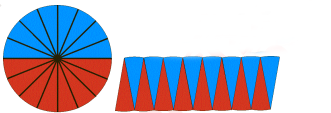
把圆32等分拼成近似的平行四边形。

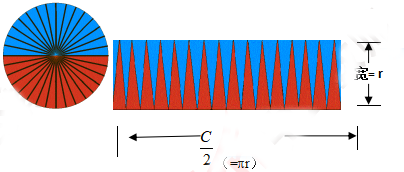
①拼成的平行四边形的高相当于圆的半径，它的底相当于圆周长的一半。

②拼成的长方形的宽相当于圆的半径，长相当于圆周长的一半。

当我们把圆平均分得的份数越多，拼成的图形就越接近于一个长方形，它的面积也就越接近了这个长方形的面积。

(4)得出结论：

问1：既然圆的面积无限接近于长方形。那么我们如何根据长方形的面积来推导圆的面积公式呢?

问2：长方形的长、宽与圆有什么关系呢?

再次展示动画。

设圆的半径为r,启发学生寻找规律,由圆的周长为2πr,推导得出长方形长为πr,宽为r,圆的面积公式:S=mr2。